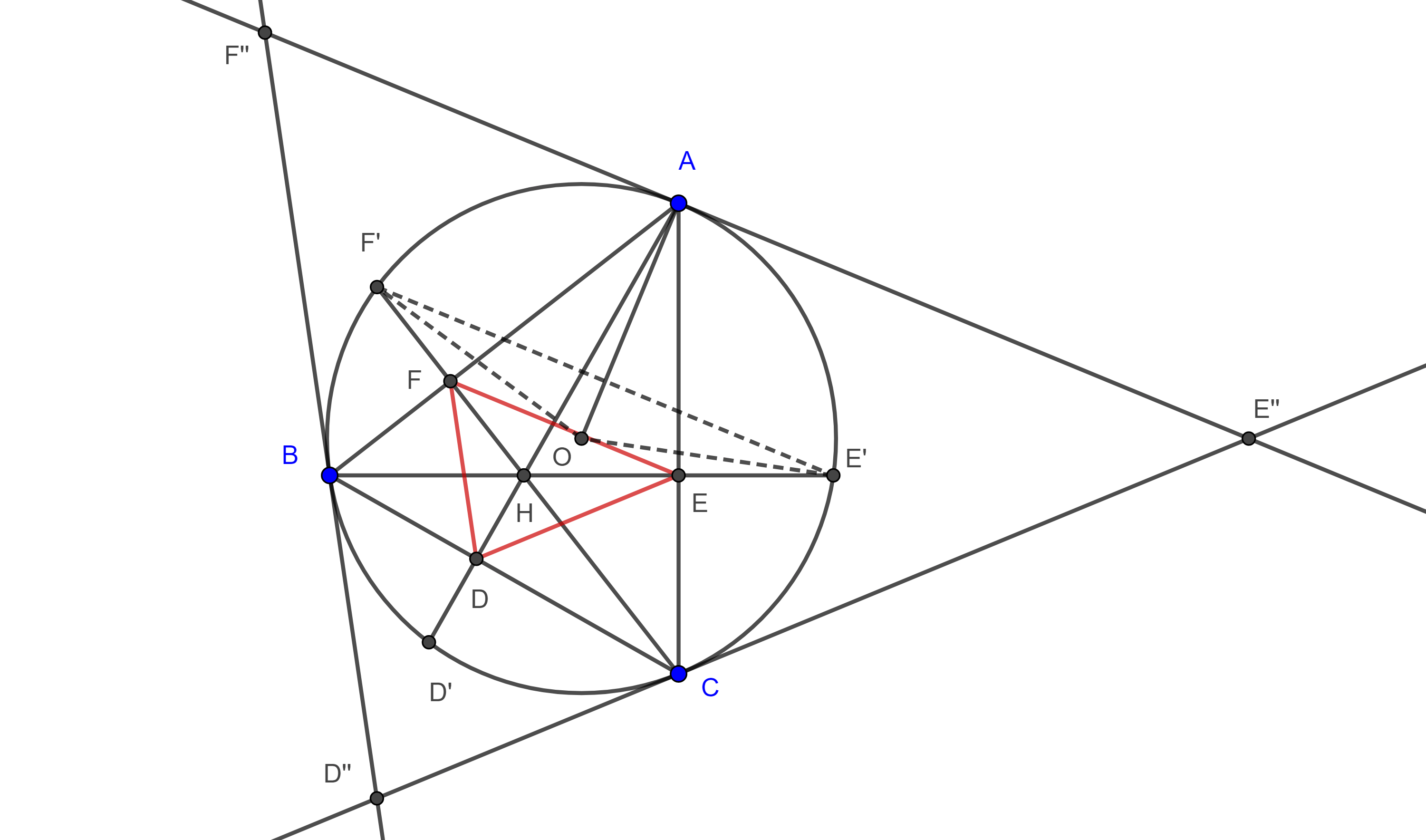
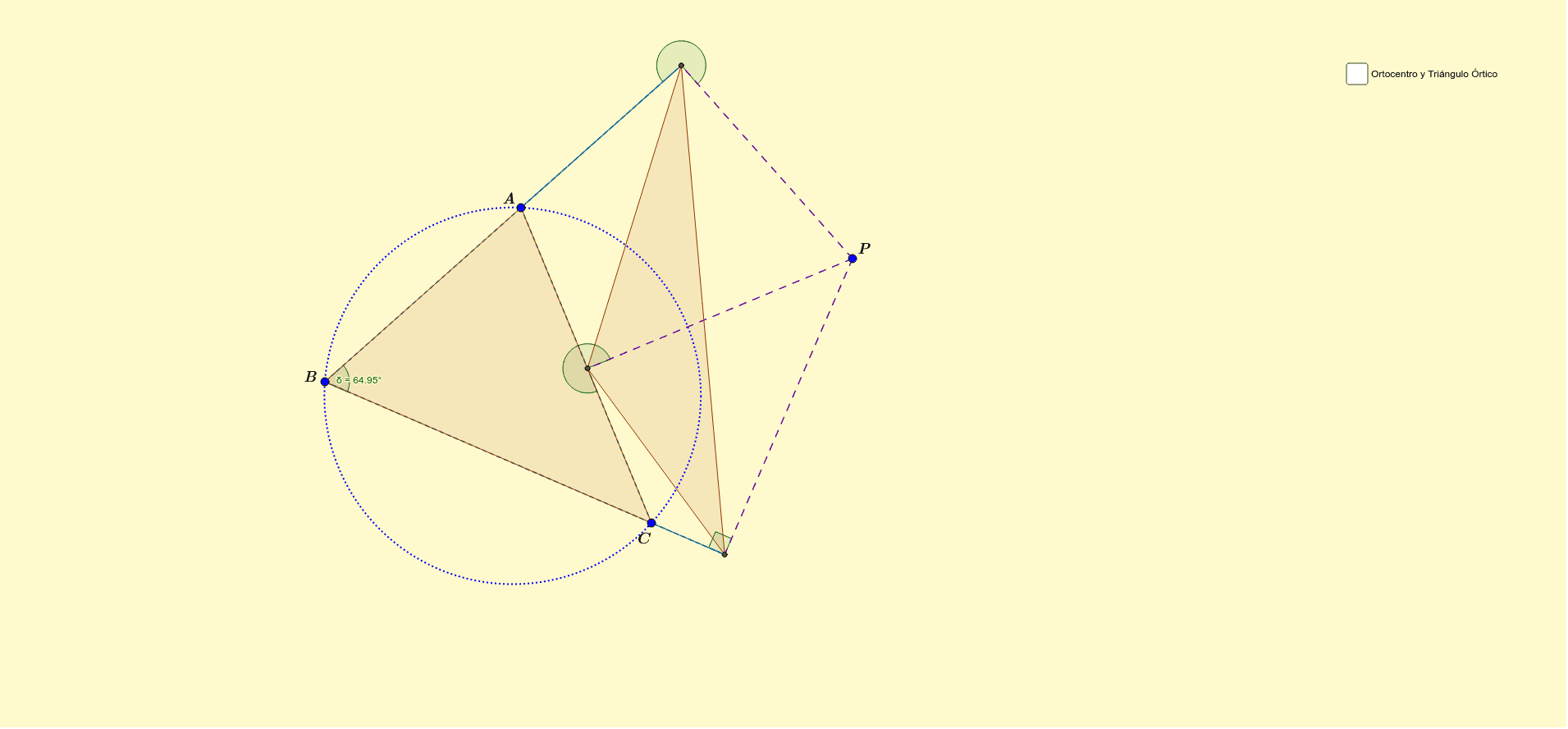
Veamos otra forma de calcularlo, llamemos h al ortocentro.
Si observamos la escena, vemos que el vector oh es la suma de los vectores oa y ah (oh=oa+ah).
Si calculamos ah, el problema está resuelto.
Supongamos que n es un vector perpendicular a bc, entonces ah=t·n.
Unos sencillos cálculos nos darán el valor de t.
Laracos math 106k subscribers subscribe construcción del ortocentro de un triángulo.
Se explica además qué es la altura de un triángulo y cómo se encuentra.
Aprenderás como usar regla y compás para.
Y la última, en ángulo recto, deslícela hacia abajo hasta que llegue a la esquina a la derecha allí.
Y si lo has hecho correctamente, usted debe encontrar que las tres alturas se cortan en un único punto y que es el ortocentro.
Mi nombre es ryan malloy y hemos discutido cómo encontrar el ortocentro de un triángulo en sencillos pasos.
Ya tenemos t, luego ya tenemos ah si tenemos n;
Pero en el plano euclídeo es fácil obtener un vector perpendicular a otro dado:
Basta intercambiar las coordenadas y cambiar de signo una de ellas.
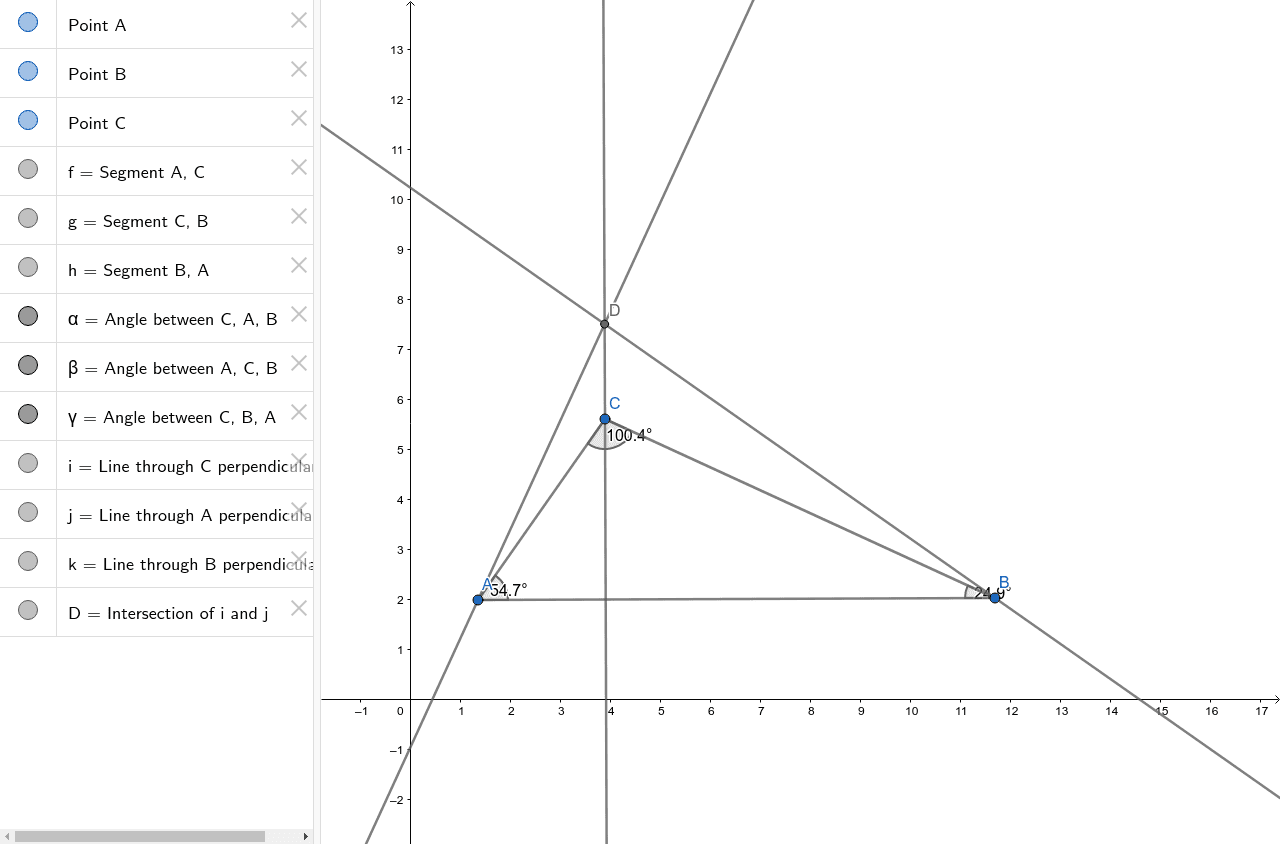
Pongamos todo esto en una escena y resolvamos con ella el problema de hallar las coordenadas del ortocentro del triángulo de vértices a(1;
Para ello trazamos rectas perpendiculares a los lados del triángulo y que pasen por el vértice opuesto al lado.
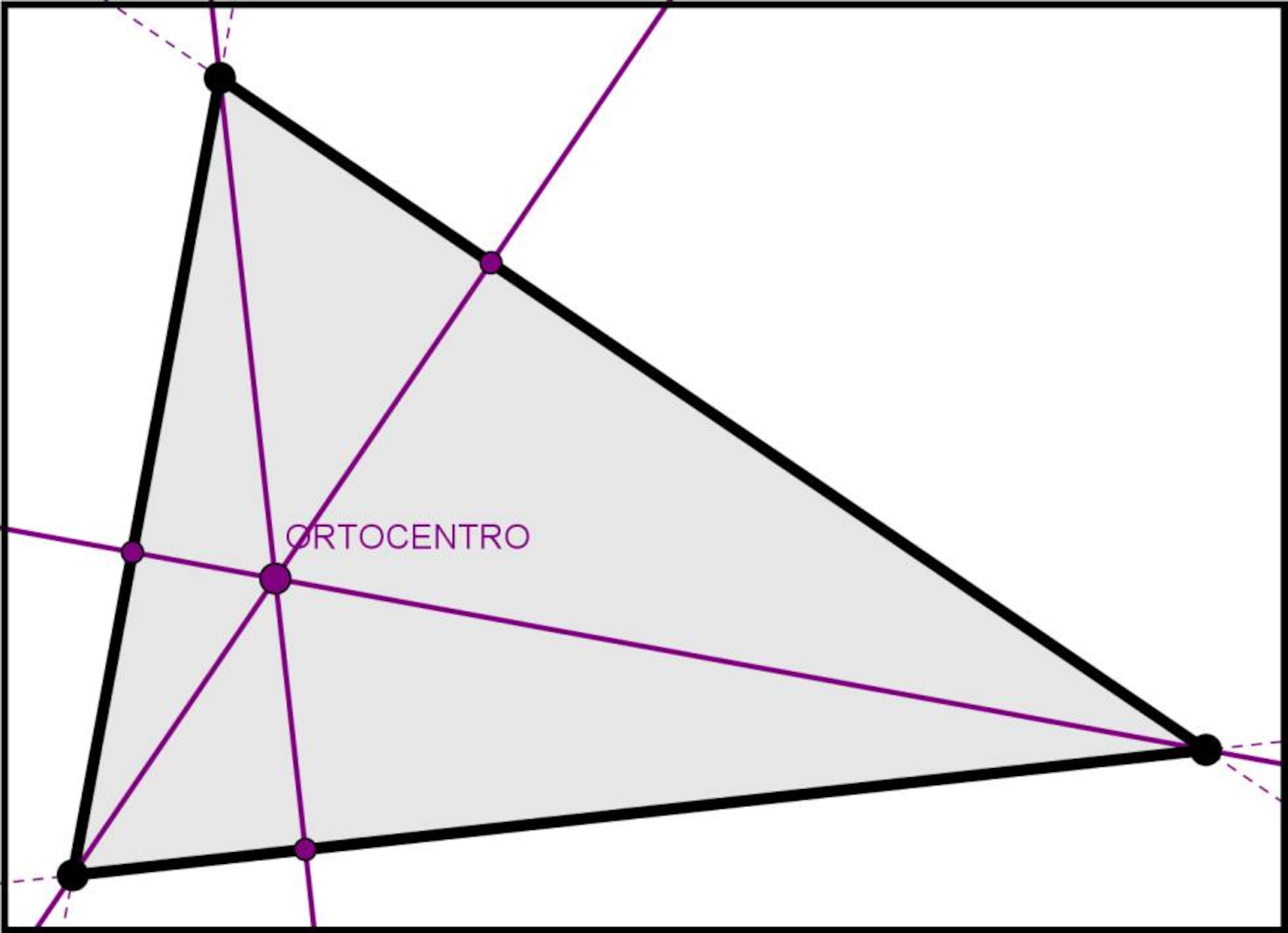
El ortocentro es el punto d.
Notar que el ortocentro se encuentra dentro del.
Cálculo del ortocentro utilizando geogebra abre geogebra y repite los pasos para calcular tu el ortocentro.
Rombicubooctaedro valor de pi teorema ssw movimientos giratorio y oscilante sesión 2 camiseta descubre temas triángulos rectángulos romboide exponente funciones escalonadas
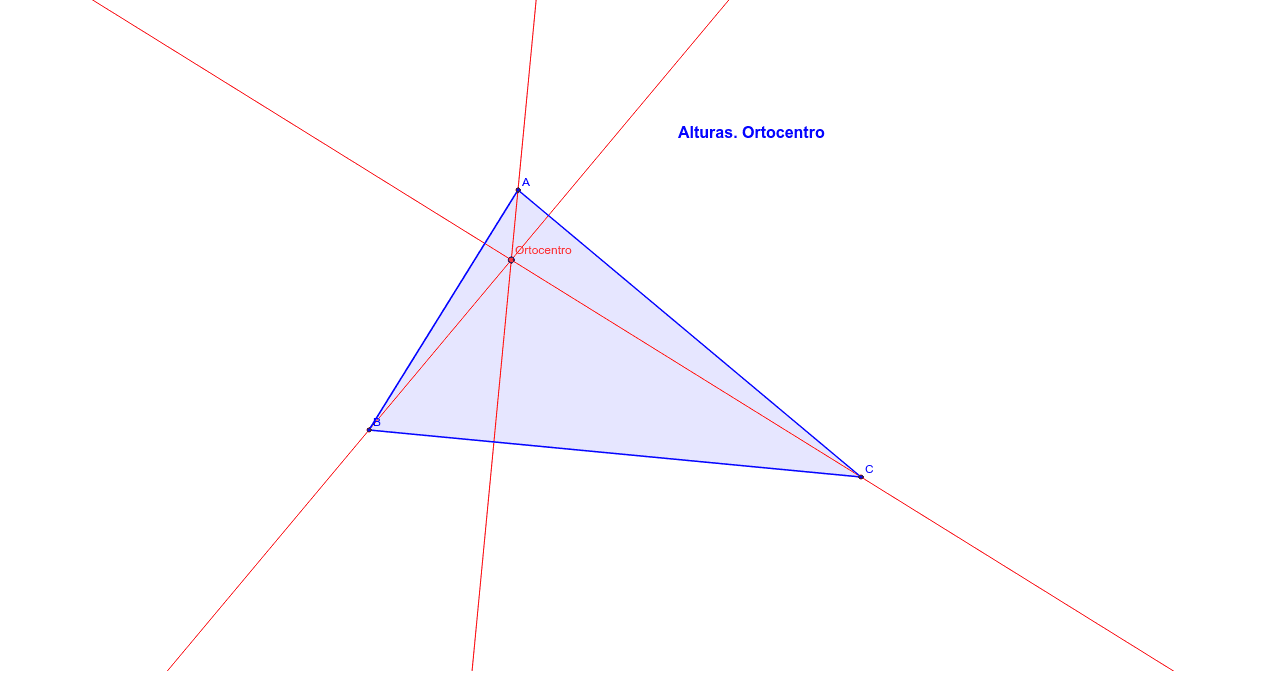
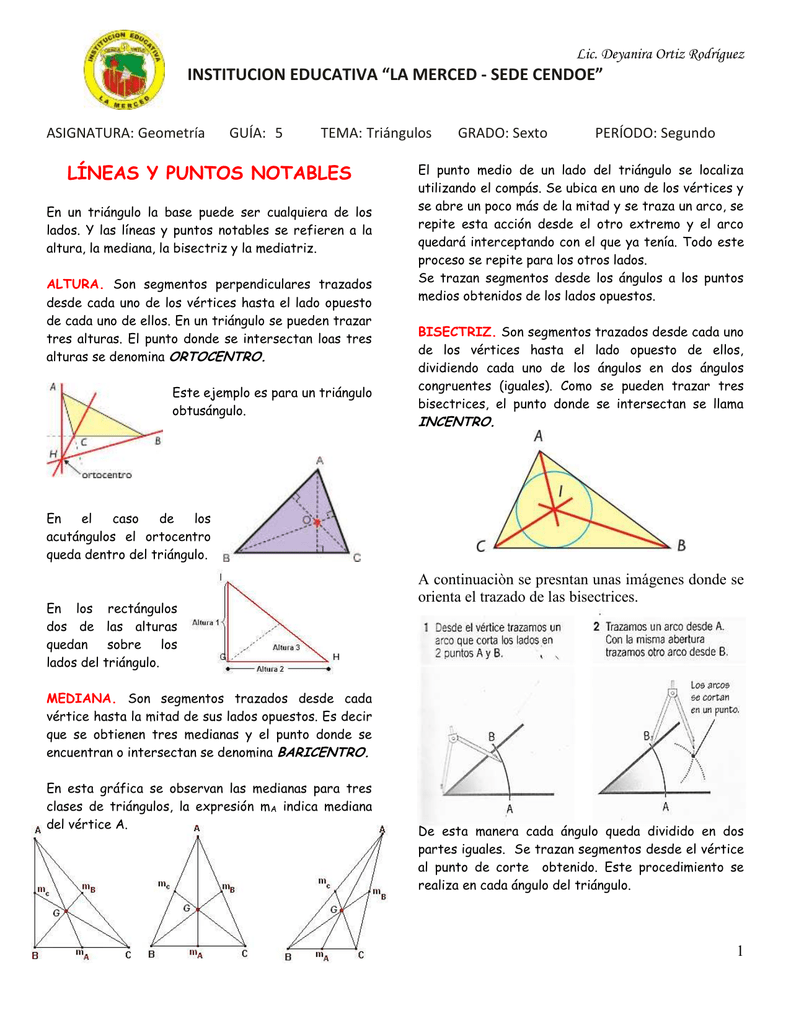
El ortocentro es la intersección de las tres alturas de un triángulo, pudiendo encontrarse dentro o fuera de la figura.
Cabe recordar que la altura de un triángulo es aquel segmento que parte de cada vértice del triángulo y se prolonga hacia su lado contrario, formando un.
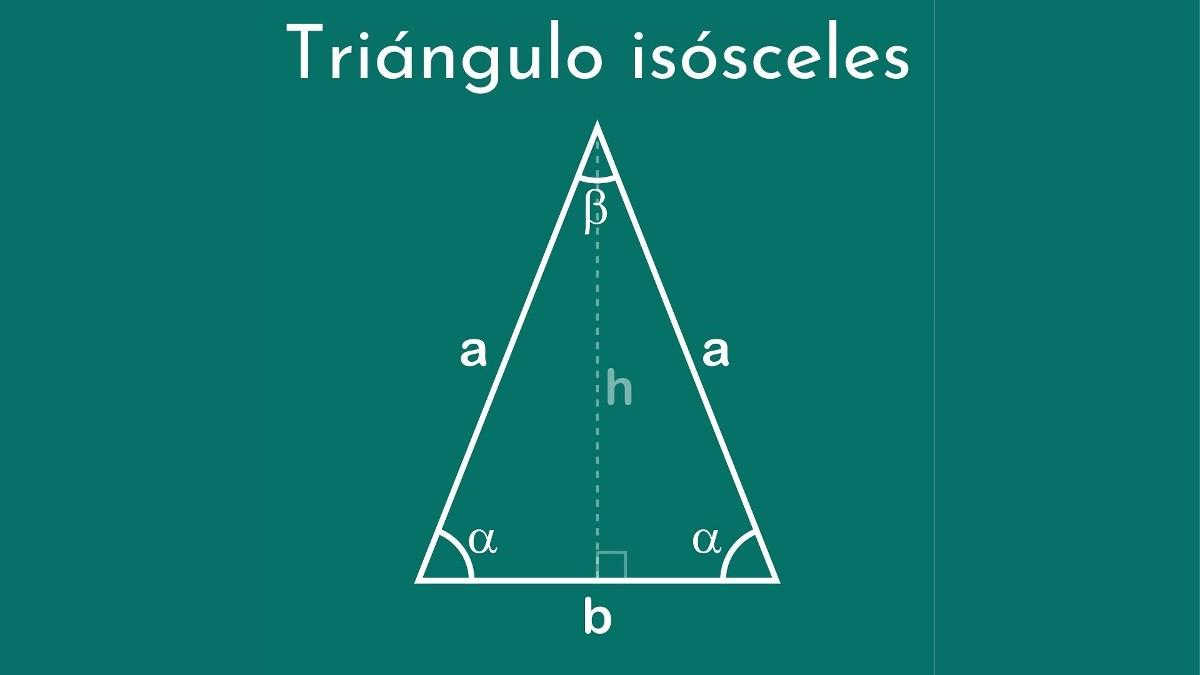
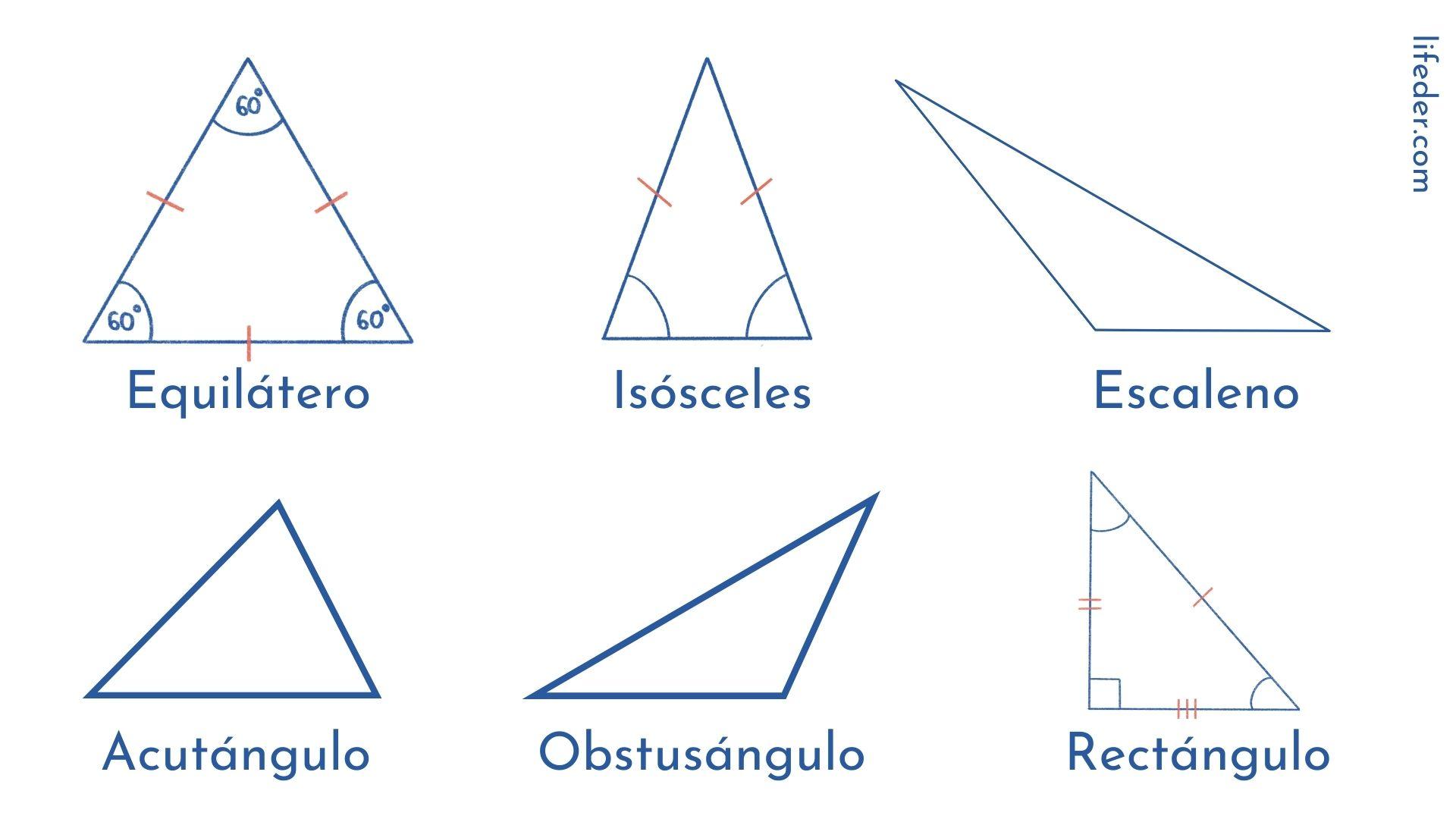
El triángulo exhibido es escaleno por el hecho de que todos sus lados miden distinto y, al unísono, es acutángulo por el hecho de que sus ángulos son inferiores que 90º.
Este género de triángulo tiene un ángulo mayor a 90° pero menos de 180º que recibe el nombre “obtuso”, y 2 ángulos agudos, los que son inferiores a 90°.
Como la altura desde c y el lado ab son perpendiculares, sus pendientes cumplen que sustituimos y despejamos la altura que pasa por tiene pendiente.
Para calcularlo, se resuelve el sistema formado por dos de las ecuaciones.
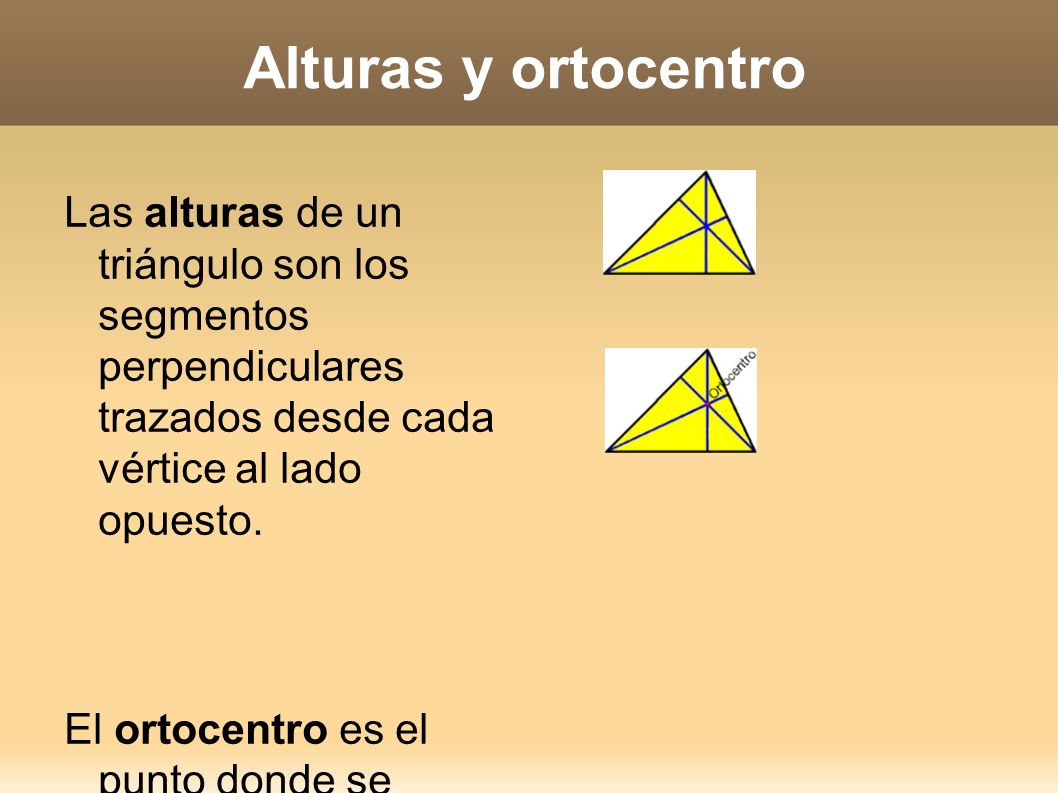
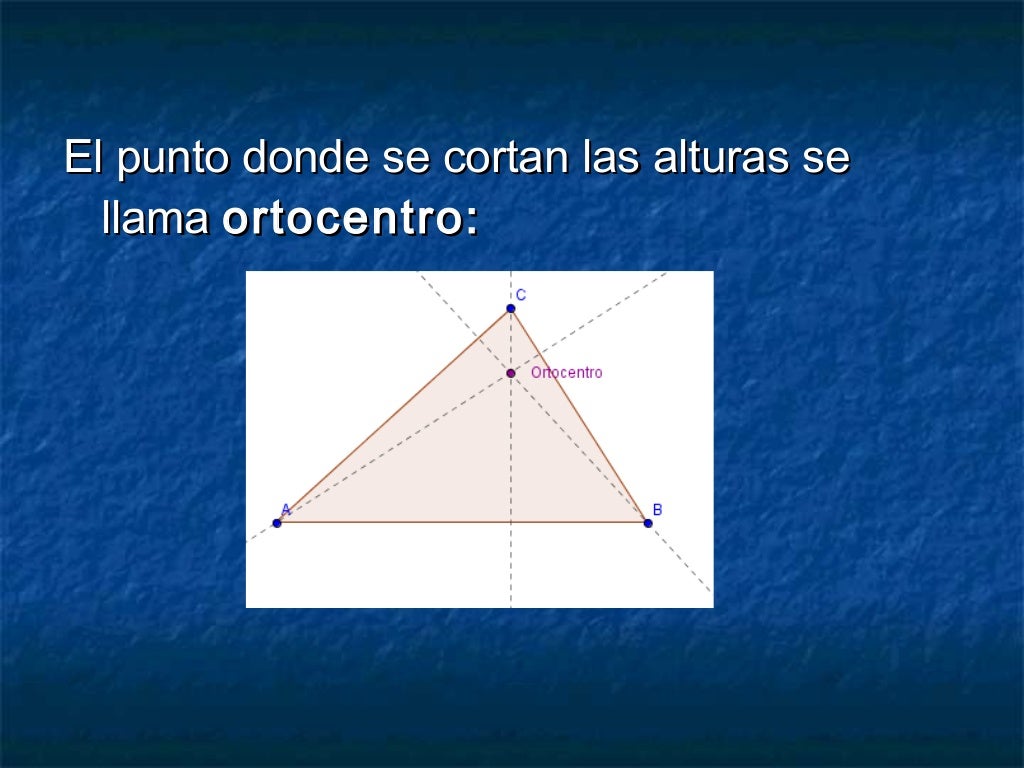
El ortocentro de un triángulo es el punto donde se cortan las tres alturas de un triángulo.
En realidad, con solo trazar dos alturas es suficiente.
Las alturas de un triángulo son perpendiculares a los lados y pasan por los vértices opuestos a esos lados.
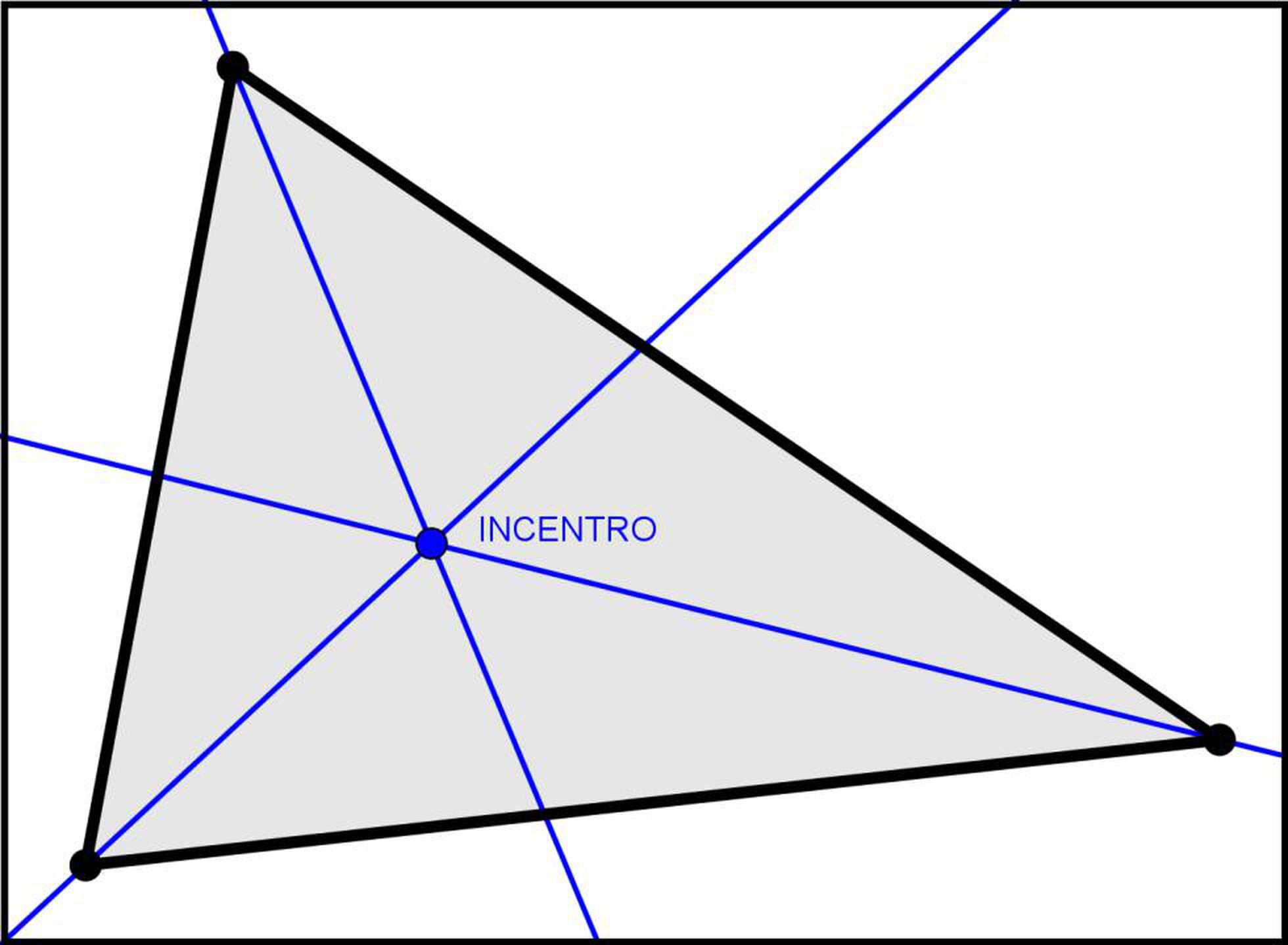
No confundir las alturas con las mediatrices.
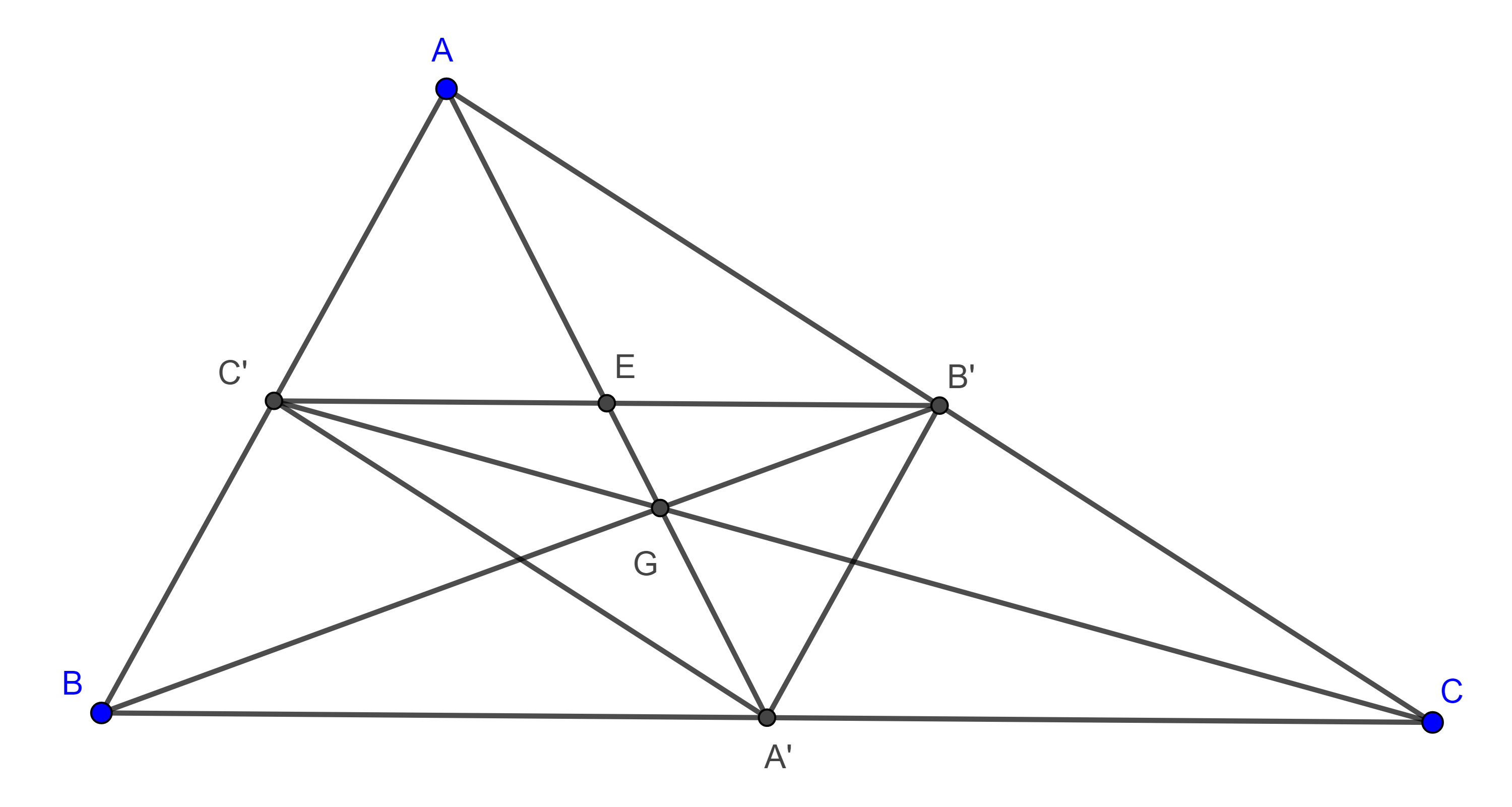
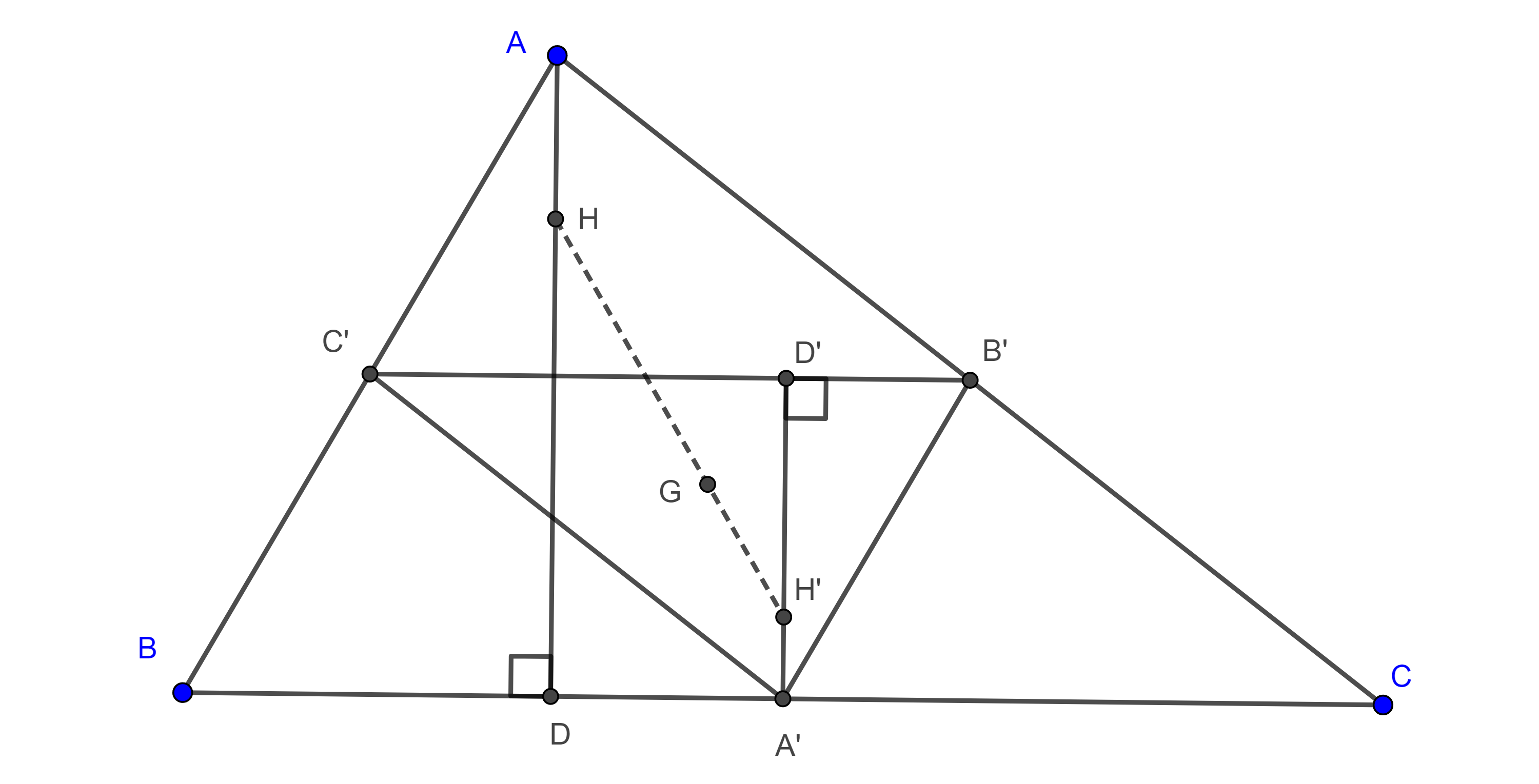
Tenemos este problema muestra que siendo un triángulo el otro centro y el centro y d coinciden entonces el triángulo equilátero va entonces el [ __ ] centro y el centro y d coinciden y como recordatorio el otro centro es donde se intersectan las alturas de un triángulo y el centro hoy de es donde se intersectan las medianas entonces aquí en la.
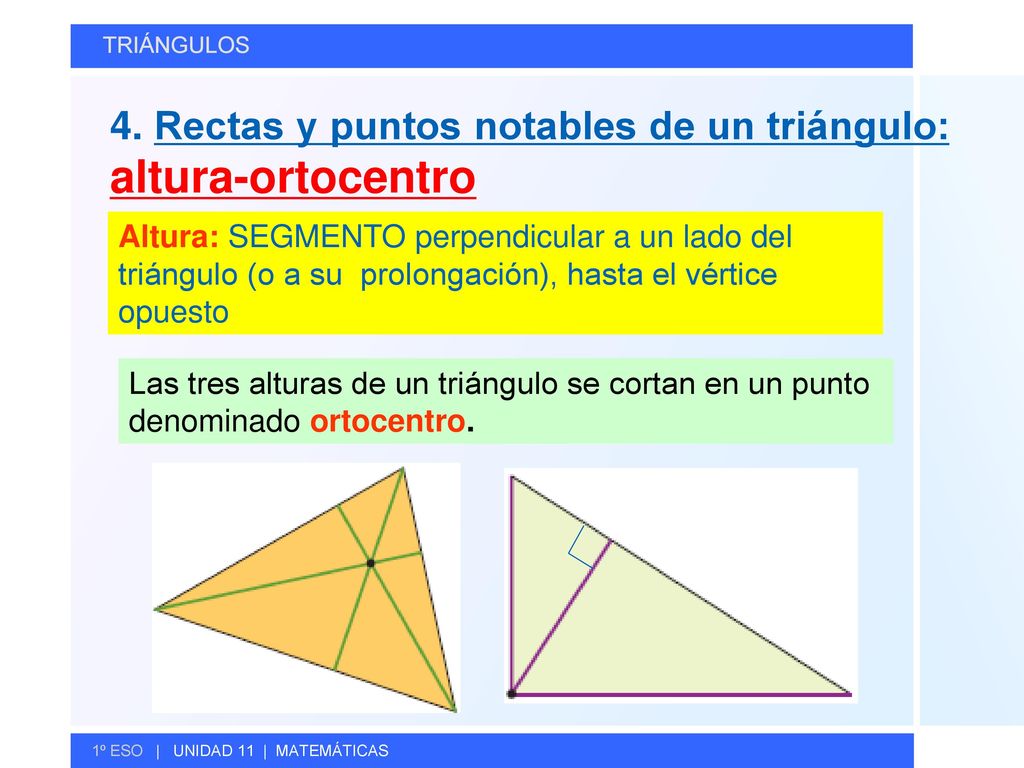
El ortocentro de un triángulo es el punto en el que se cruzan las perpendiculares trazadas desde los vértices a los lados opuestos del triángulo.
Para un triángulo de ángulo agudo, el ortocentro se encuentra dentro del triángulo.
Para el triángulo de ángulo obtuso, el ortocentro se encuentra fuera del triángulo.
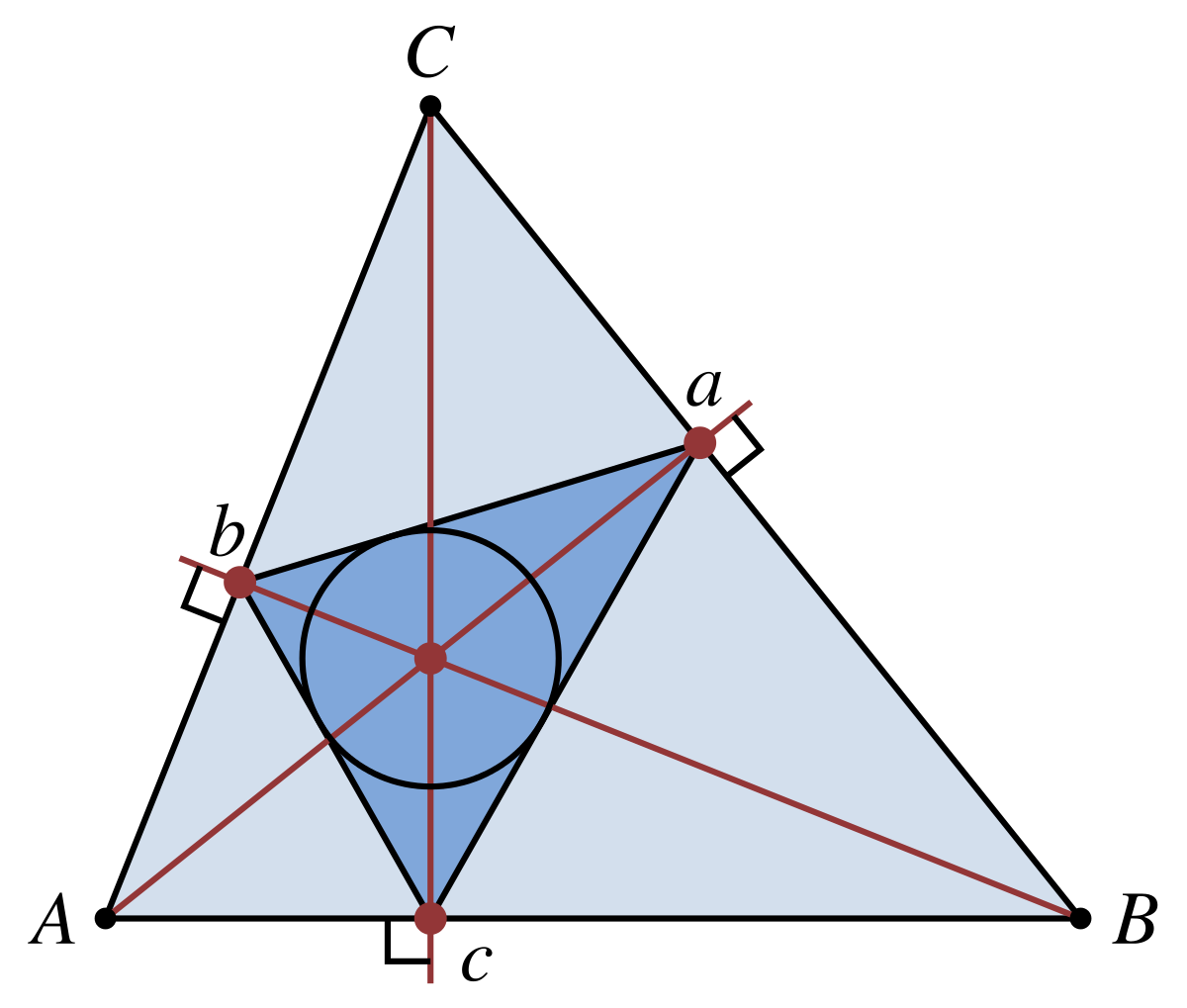
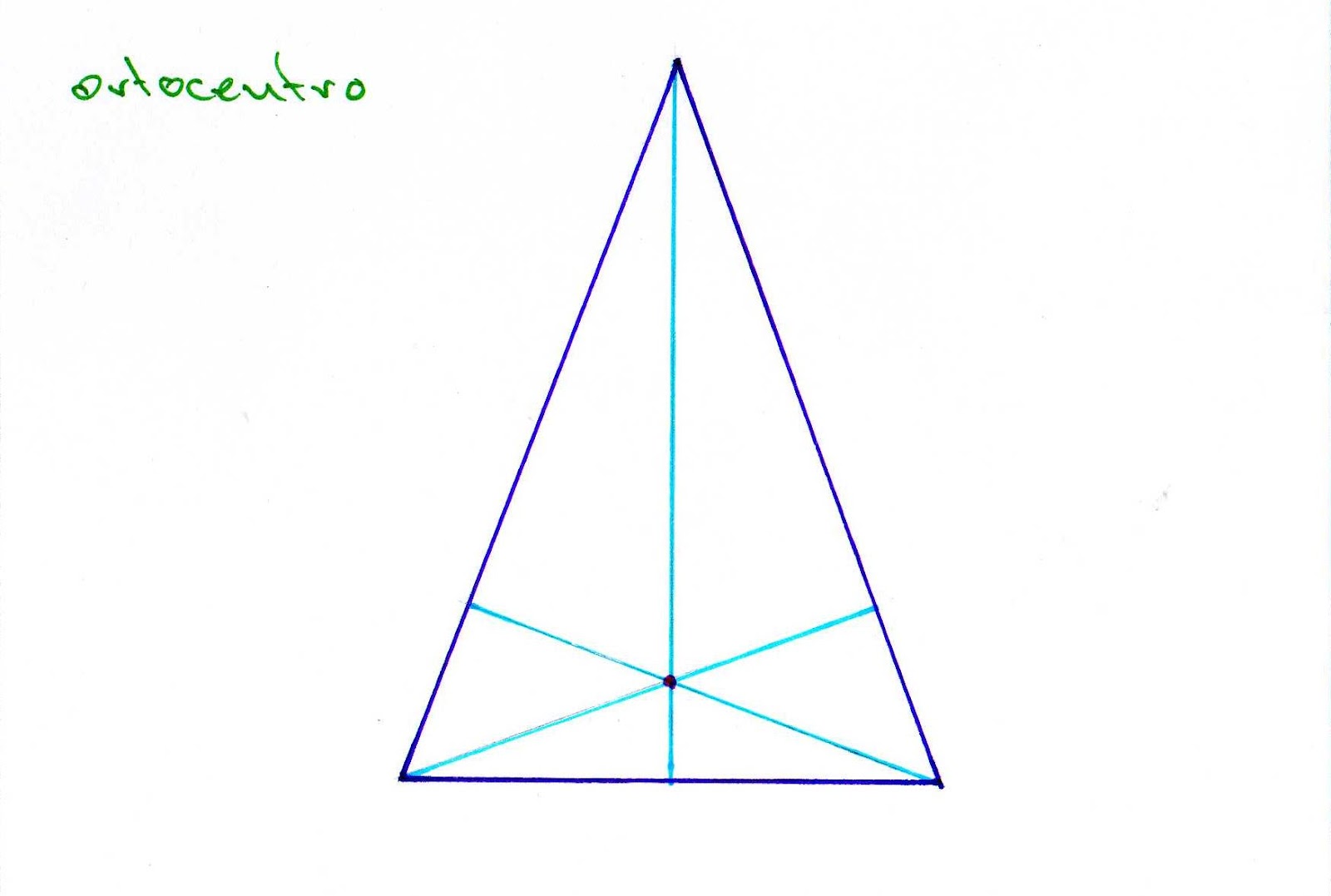
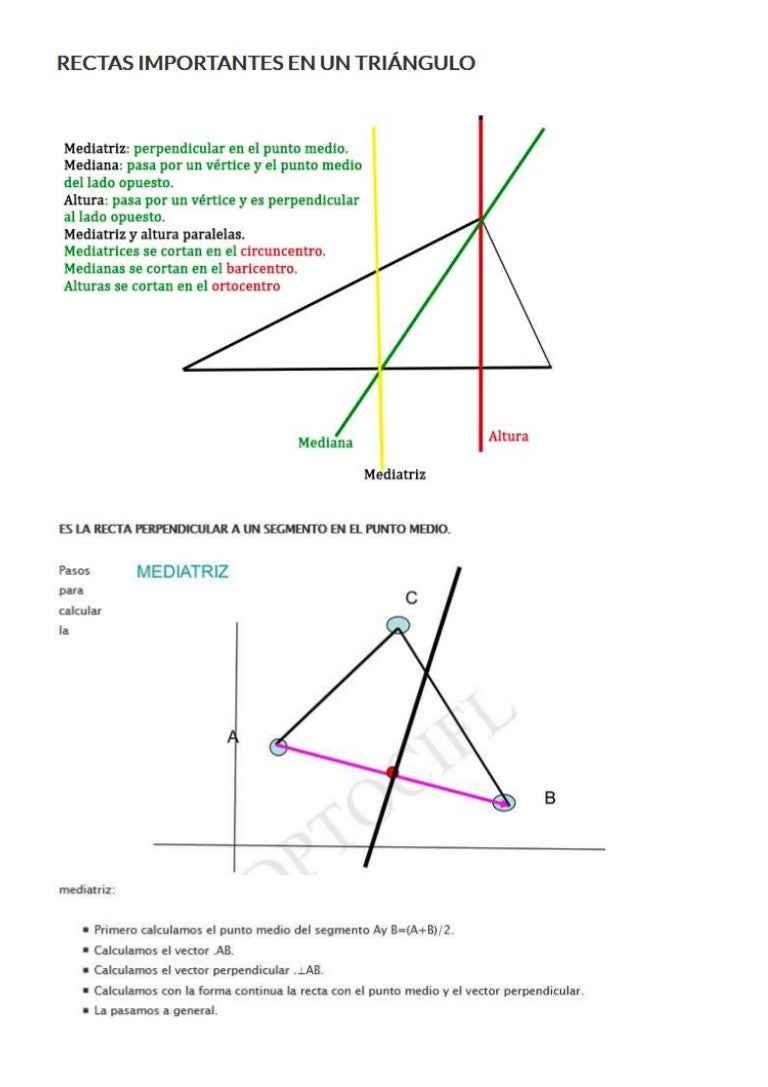
Ortocentro es el punto de corte de las tres alturas.
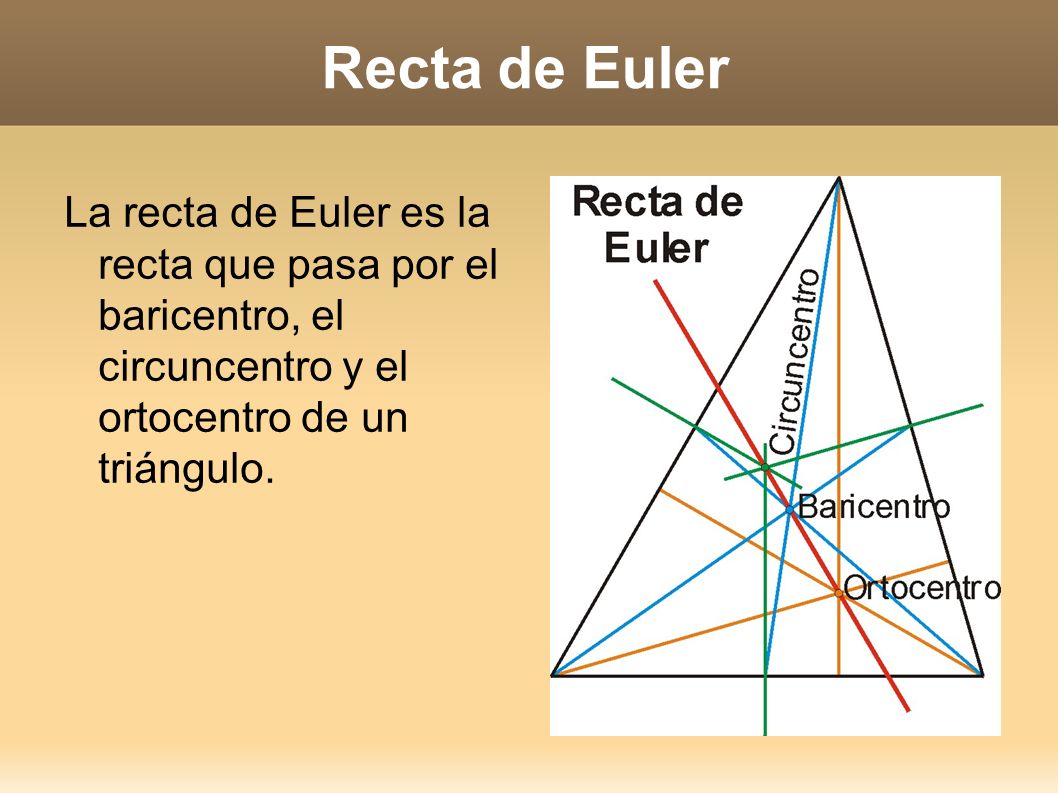
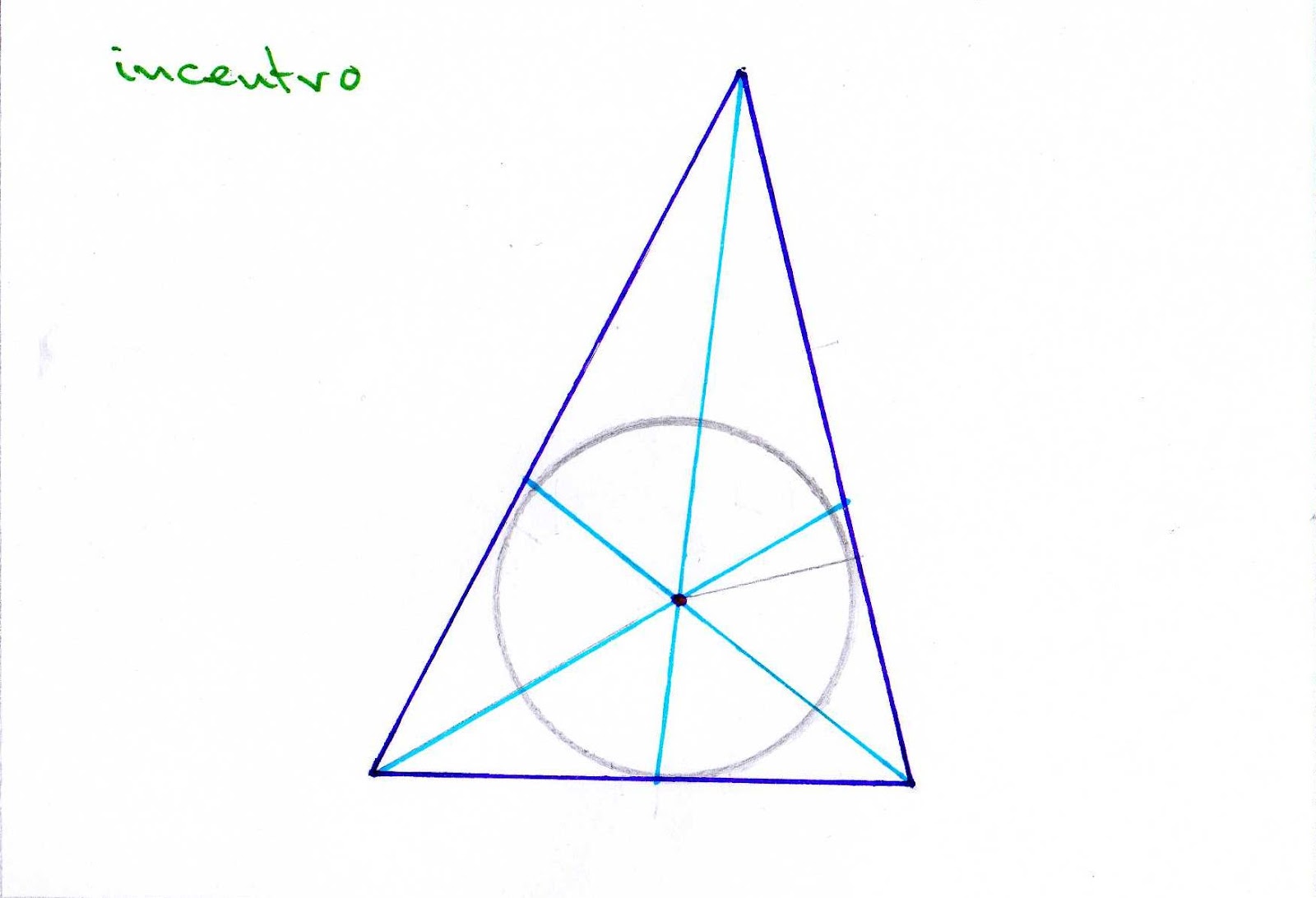
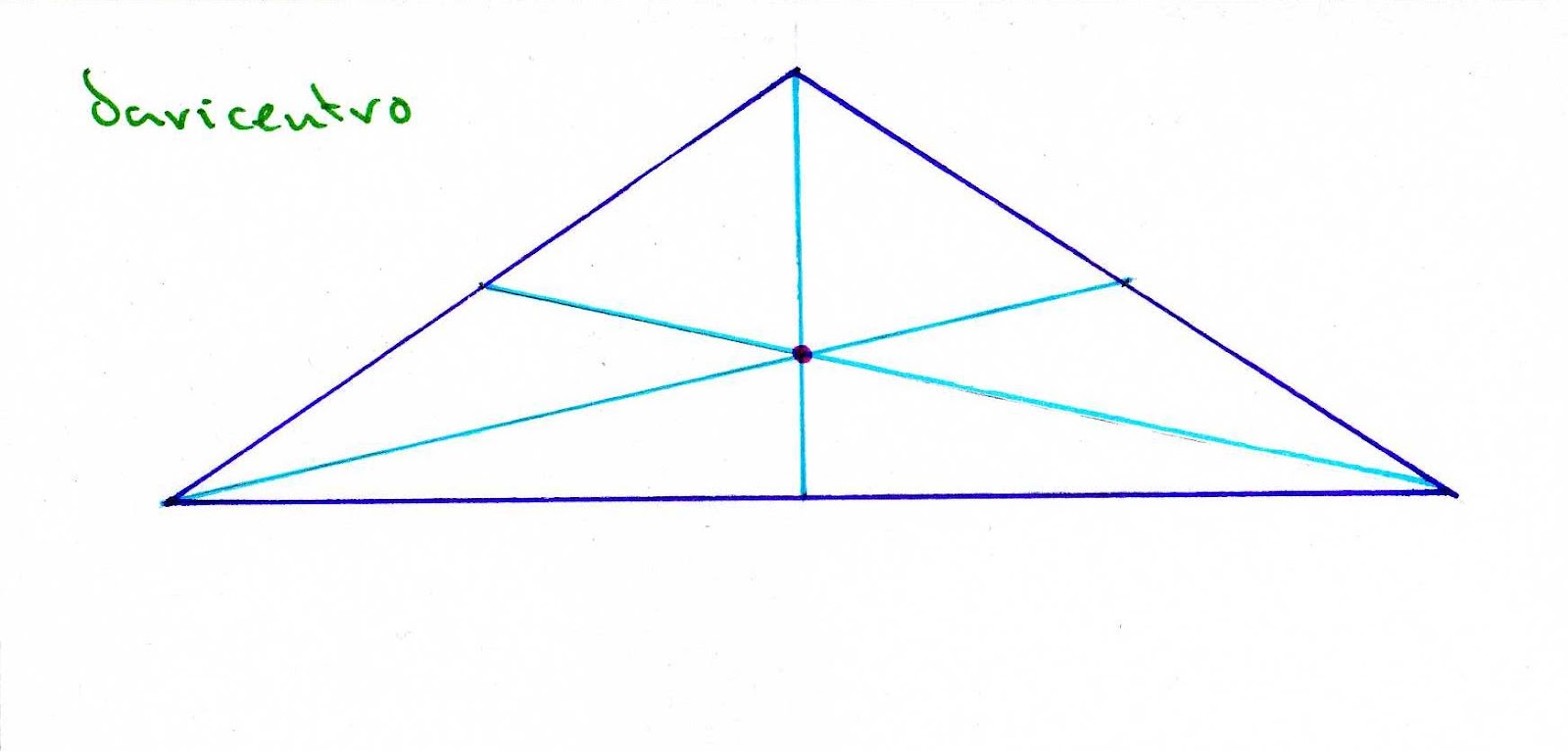
Medianas de un triángulo mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
Baricentro es el punto de corte de las tres medianas.